What is the Trigonometric ratio for sine Z — Explanation & Interactive Diagram

What is the Trigonometric ratio for sine Z? In this section we explain the definition, show a live diagram you can interact with, provide examples, and answer common questions — all focused on the phrase What is the Trigonometric ratio for sine Z.

Definition — What is the Trigonometric ratio for sine Z?

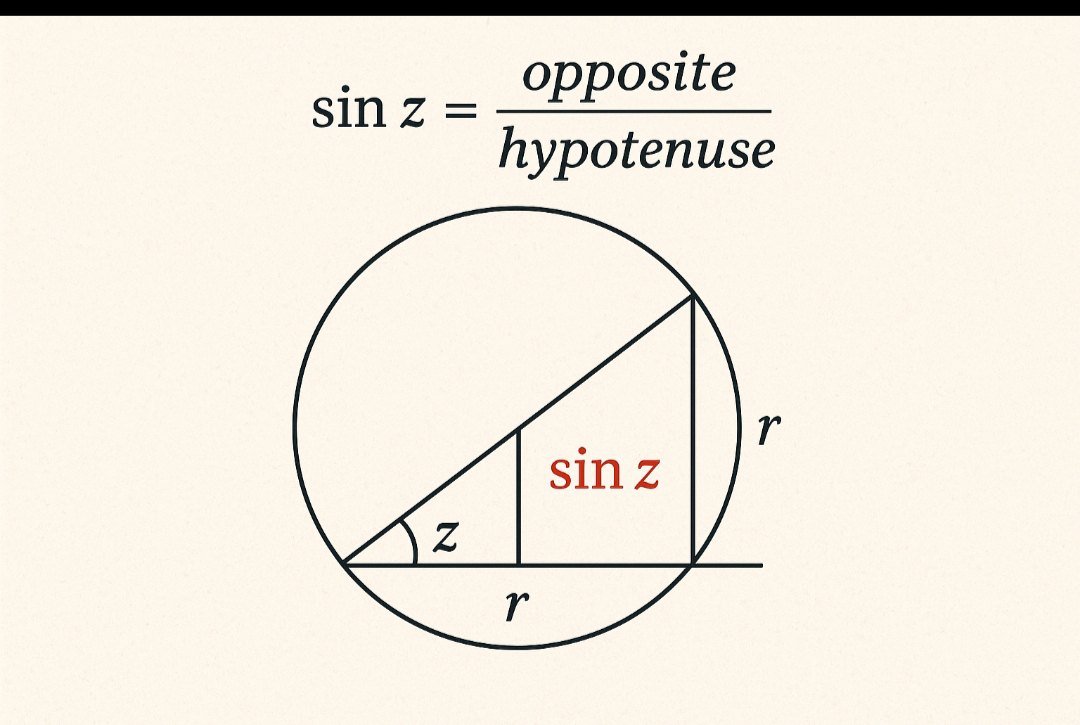
By definition, the trigonometric ratio for sine Z (written sin Z) is the ratio of the length of the side opposite angle Z to the hypotenuse in a right triangle:

sin Z = opposite / hypotenuse

On the unit circle (radius = 1), sin Z equals the y-coordinate of the point reached by rotating from the positive x-axis by angle Z (measured in degrees or radians).

Unit circle diagram (interactive)

Move the slider to change Z (angle) and watch the point move — the y-value displayed is sin Z, illustrating What is the Trigonometric ratio for sine Z.

Properties & formulas (using the keyword)

Basic identities including “What is the Trigonometric ratio for sine Z”

• sin²Z + cos²Z = 1
• sin(-Z) = -sin Z
• sin(90° − Z) = cos Z
• sin(A ± B) = sin A cos B ± cos A sin B

Worked examples — answering “What is the Trigonometric ratio for sine Z”

1. Right triangle: If the opposite = 3 and hypotenuse = 5, sin Z = 3/5 = 0.6.
2. Unit circle: Z = 30° → sin 30° = 0.5.
3. Using identities: If cos Z = 0.8 and Z in first quadrant, sin Z = sqrt(1 - 0.8²) = 0.6.

Frequently asked questions — What is the Trigonometric ratio for sine Z (20)

1. What is the trigonometric ratio for sine Z in words?

Sin Z is the ratio of the side opposite angle Z to the hypotenuse (in a right triangle), or the y-coordinate on the unit circle.

2. How do I calculate sin Z from a right triangle?

Divide the length of the opposite side by the hypotenuse: sin Z = opposite / hypotenuse.

3. What is sin 90° for Z = 90°?

sin 90° = 1.

4. Can sin Z be negative?

Yes — sin Z is negative when Z is in quadrants III and IV (angles between 180°–360°).

5. What units can Z be in?

Z can be in degrees or radians (e.g., 180° = π radians).

6. What are common exact values of sin Z?

sin 0°=0, sin 30°=1/2, sin 45°=√2/2, sin 60°=√3/2, sin 90°=1.

7. How does the unit circle show “What is the Trigonometric ratio for sine Z”?

On the unit circle, sin Z is the vertical coordinate (y-value) of the point at angle Z.

8. Is sin Z periodic?

Yes, sin Z repeats every 360° (2π radians): sin(Z + 360°) = sin Z.

9. How to compute sin Z on a calculator?

Set the correct unit (deg/rad), enter the angle Z, then press the sin function.

10. What is the derivative of sin Z?

d/dZ [sin Z] = cos Z (using Z in radians).

11. What is the integral of sin Z?

∫ sin Z dZ = −cos Z + C (for Z in radians).

12. How to find angle Z if sin Z is known?

Use the inverse sine (arcsin) function: Z = arcsin(value), paying attention to the correct quadrant.

13. Can sin Z = 2?

No — sine values are bounded between −1 and 1.

14. Relationship between sin Z and cos Z?

sin²Z + cos²Z = 1 always holds.

15. What is sin(180° − Z)?

sin(180° − Z) = sin Z (sine is symmetric about 90°).

16. Common mistakes when using sin Z?

Using degrees vs radians incorrectly and misidentifying which side is opposite or hypotenuse in triangle problems.

17. How to express sin Z in terms of complex exponentials?

sin Z = (e^{iZ} − e^{−iZ}) / (2i), when Z is in radians.

18. How is sin Z used in real-world contexts?

Wave motion, signal processing, engineering, navigation, and any periodic phenomena use sine functions.

19. Can you compute sin Z from coordinates?

Yes: for a point (x,y) on the unit circle at angle Z, sin Z = y.

20. Where else should I learn about sin Z?

Good resources include math textbooks, Khan Academy, and university lecture notes (links below).

Resources links

Internal page: Explore Detailed study of Trigonometry (internal)
Outbound resource: Khan Academy — Trigonometry